Teori himpunan merupakan fondasi penting dalam matematika. Konsep ini membahas tentang kumpulan objek yang memiliki sifat tertentu, membentuk dasar untuk memahami berbagai konsep matematika yang lebih kompleks.

Dengan memahami pengertian himpunan dalam matematika, pembaca dapat memperoleh dasar yang kuat untuk memahami konsep-konsep yang lebih lanjut. Artikel ini akan membahas secara komprehensif tentang teori ini, mulai dari definisi hingga aplikasinya dalam berbagai bidang.
Poin Kunci
- Memahami definisi dasar teori himpunan.
- Mengenal pentingnya himpunan dalam matematika.
- Mengidentifikasi aplikasi teori himpunan dalam berbagai bidang.
- Menganalisis bagaimana teori himpunan membentuk dasar untuk konsep matematika yang lebih kompleks.
- Mengetahui bagaimana memahami himpunan dapat meningkatkan pemahaman matematika.
Pengertian Teori Himpunan
Teori himpunan merupakan fondasi dasar dalam matematika yang mempelajari kumpulan objek dengan sifat tertentu. Dalam matematika, teori ini digunakan sebagai dasar untuk memahami berbagai konsep seperti relasi, fungsi, dan struktur aljabar.
Definisi Himpunan
Himpunan didefinisikan sebagai kumpulan objek yang unik dan memiliki sifat tertentu. Objek-objek dalam himpunan disebut elemen atau anggota himpunan. Notasi himpunan biasanya digunakan untuk menyatakan keanggotaan suatu objek dalam himpunan.
Sebagai contoh, jika kita memiliki himpunan A yang berisi angka 1, 2, dan 3, maka kita dapat menulisnya sebagai A = {1, 2, 3}. Ini berarti bahwa 1, 2, dan 3 adalah elemen dari himpunan A.
Penerapan dalam Matematika
Teori himpunan memiliki penerapan yang luas dalam matematika. Salah satu contoh penerapannya adalah dalam definisi relasi dan fungsi. Relasi antara dua himpunan dapat didefinisikan sebagai subset dari produk Cartesius kedua himpunan tersebut.
Selain itu, teori himpunan juga digunakan dalam memahami struktur aljabar seperti grup, ring, dan field. Dengan menggunakan konsep himpunan, kita dapat memahami sifat-sifat dan operasi-operasi dalam struktur aljabar tersebut.
“Teori himpunan adalah bahasa dasar matematika; ia menyediakan sarana untuk definisi yang tepat dari konsep matematika.”
Sejarah Teori Himpunan
Sejarah teori himpunan dimulai pada akhir abad ke-19 dengan kontribusi dari beberapa matematikawan terkemuka. Teori himpunan telah berkembang pesat dan menjadi dasar bagi berbagai cabang matematika.
Tokoh-Tokoh Penting
Tokoh-tokoh seperti Georg Cantor dan Ernst Zermelo berperan besar dalam mengembangkan teori himpunan. Georg Cantor memperkenalkan konsep himpunan tak terhingga dan mengembangkan teori himpunan modern.
Ernst Zermelo, di sisi lain, memberikan kontribusi signifikan melalui aksioma Zermelo-Fraenkel yang menjadi dasar teori himpunan modern.
Perkembangan Teori
Perkembangan teori himpunan tidak hanya mempengaruhi matematika murni tetapi juga berbagai bidang lainnya seperti statistika dan informatika. Teori himpunan memberikan dasar bagi berbagai konsep matematika yang lebih kompleks.
| Tokoh | Kontribusi |
|---|---|
| Georg Cantor | Mengembangkan teori himpunan modern dan konsep himpunan tak terhingga |
| Ernst Zermelo | Mengembangkan aksioma Zermelo-Fraenkel sebagai dasar teori himpunan |
Dengan demikian, teori himpunan terus berkembang dan memberikan dampak signifikan pada berbagai bidang ilmu pengetahuan.
Notasi dan Simbol Himpunan
Notasi dan simbol himpunan memainkan peran penting dalam memahami konsep matematika yang melibatkan himpunan. Dengan menggunakan notasi yang baku, kita dapat dengan mudah mengkomunikasikan ide-ide matematika yang kompleks.
Simbol Dasar dalam Teori Himpunan
Simbol-simbol seperti ∈, ⊆, dan ∪ digunakan untuk menyatakan relasi antara elemen dan himpunan. Simbol ∈ digunakan untuk menunjukkan bahwa suatu elemen adalah anggota dari suatu himpunan.
Contoh: Jika A = {1, 2, 3}, maka 1 ∈ A berarti 1 adalah elemen dari himpunan A.
Notasi Himpunan
Notasi himpunan yang baku memudahkan penulisan dan komunikasi konsep-konsep matematika. Himpunan dapat dinotasikan dengan menggunakan kurung kurawal { }.
Contoh: Himpunan bilangan genap dapat dinotasikan sebagai G = {2, 4, 6, …}.
Berikut adalah tabel yang merangkum beberapa notasi dan simbol himpunan yang umum digunakan:
| Simbol | Arti | Contoh |
|---|---|---|
| ∈ | Elemen dari | 1 ∈ {1, 2, 3} |
| ⊆ | Himpunan bagian dari | {1, 2} ⊆ {1, 2, 3} |
| ∪ | Gabungan himpunan | {1, 2} ∪ {2, 3} = {1, 2, 3} |
Dengan memahami notasi dan simbol himpunan, kita dapat lebih mudah dalam mengoperasikan himpunan dan memahami konsep-konsep yang lebih lanjut dalam matematika.
Jenis-Jenis Himpunan
Dalam teori himpunan, terdapat beberapa jenis himpunan yang memiliki karakteristik unik dan memainkan peran penting dalam berbagai aplikasi matematika.
Himpunan Kosong
Himpunan kosong adalah himpunan yang tidak memiliki elemen. Himpunan ini dilambangkan dengan {} atau ∅. Himpunan kosong merupakan konsep dasar dalam teori himpunan karena sering digunakan sebagai acuan dalam berbagai operasi himpunan.
Himpunan Berhingga dan Tak Terhingga
Himpunan dapat dibedakan menjadi himpunan berhingga dan tak terhingga berdasarkan jumlah elemennya. Himpunan berhingga memiliki jumlah elemen yang terbatas, sedangkan himpunan tak terhingga memiliki jumlah elemen yang tidak terbatas.
Contoh himpunan berhingga adalah himpunan bilangan asli kurang dari 10, yaitu {1, 2, 3, 4, 5, 6, 7, 8, 9}. Sementara itu, himpunan bilangan asli merupakan contoh himpunan tak terhingga karena memiliki elemen yang tak terhingga banyaknya.
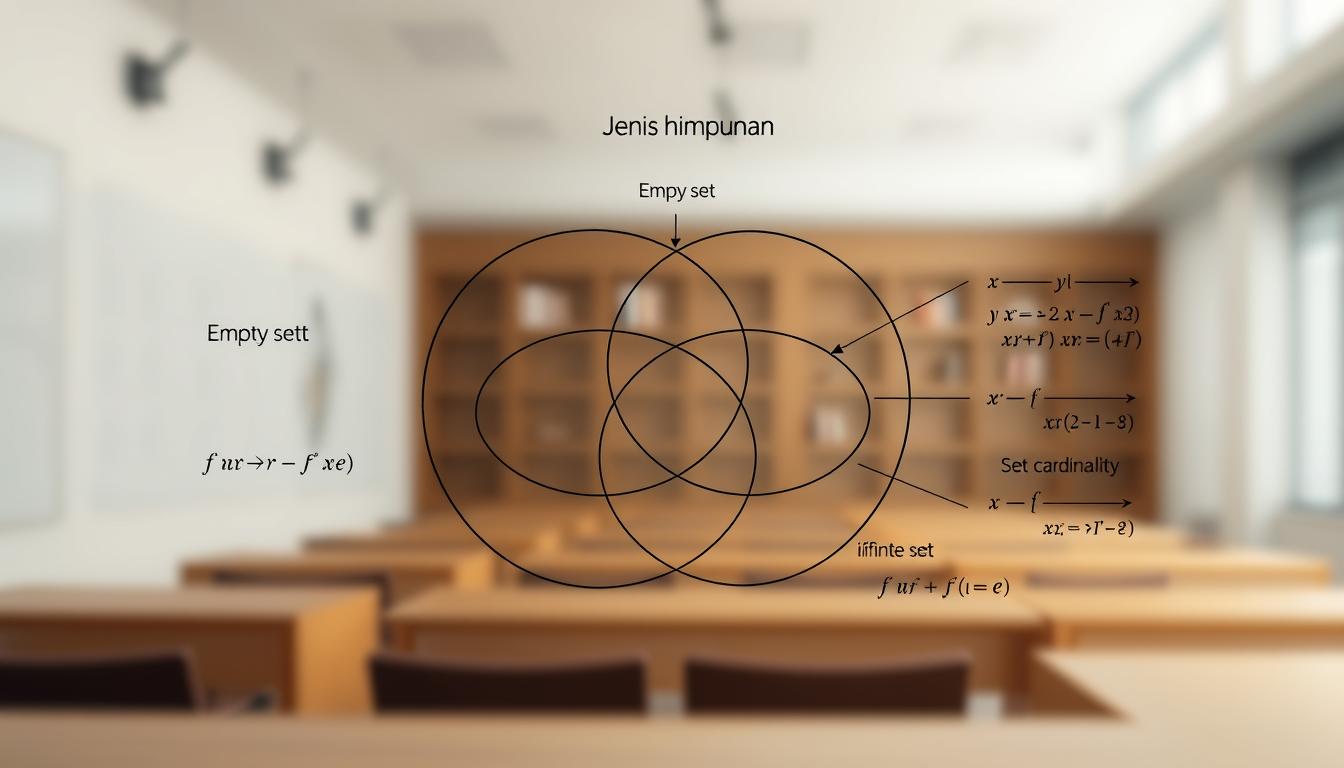
Himpunan Bagian
Himpunan bagian atau subset adalah himpunan yang elemennya merupakan bagian dari himpunan lainnya. Misalnya, jika kita memiliki himpunan A = {1, 2, 3}, maka himpunan B = {1, 2} adalah himpunan bagian dari A karena semua elemen B terdapat dalam A.
Penting untuk memahami konsep himpunan bagian karena banyak digunakan dalam berbagai operasi himpunan dan teori matematika lainnya.
Operasi pada Himpunan
Operasi pada himpunan merupakan dasar dalam memahami berbagai konsep matematika yang lebih kompleks. Operasi-operasi ini memungkinkan kita untuk memanipulasi himpunan dan mendapatkan hasil yang diinginkan.
Union (Gabungan) Himpunan
Union atau gabungan himpunan adalah operasi yang menghasilkan himpunan baru yang berisi semua elemen dari himpunan yang dioperasikan. Misalnya, jika kita memiliki dua himpunan A dan B, maka union dari A dan B (ditulis sebagai A ∪ B) berisi semua elemen yang ada di A, di B, atau di kedua himpunan tersebut.
Contoh: Jika A = {1, 2, 3} dan B = {3, 4, 5}, maka A ∪ B = {1, 2, 3, 4, 5}. Operasi union himpunan ini sangat berguna dalam menggabungkan data dari beberapa sumber.
Intersection (Irisan) Himpunan
Intersection atau irisan himpunan adalah operasi yang menghasilkan himpunan baru yang berisi elemen-elemen yang sama di antara himpunan yang dioperasikan. Misalnya, intersection dari A dan B (ditulis sebagai A ∩ B) berisi elemen-elemen yang ada di kedua himpunan A dan B.
Contoh: Jika A = {1, 2, 3} dan B = {3, 4, 5}, maka A ∩ B = {3}. Operasi intersection himpunan ini berguna untuk menemukan kesamaan antara dua set data.
Complement (Pelengkap) Himpunan
Complement atau pelengkap himpunan adalah operasi yang menghasilkan himpunan baru yang berisi elemen-elemen yang tidak ada di himpunan lainnya, tetapi ada di himpunan semesta yang didefinisikan. Complement dari A (ditulis sebagai A atau A’) berisi semua elemen di himpunan semesta S yang tidak ada di A.
Contoh: Jika S = {1, 2, 3, 4, 5} dan A = {1, 2}, maka A = {3, 4, 5}. Operasi complement ini membantu dalam mengidentifikasi elemen-elemen yang tidak termasuk dalam himpunan tertentu.
Diagram Venn dan Penerapannya
Diagram Venn merupakan alat visual yang efektif untuk memahami relasi antara himpunan. Dengan menggunakan diagram ini, kita dapat memvisualisasikan konsep-konsep himpunan seperti union, intersection, dan complement dengan lebih jelas.
Pengertian Diagram Venn
Diagram Venn adalah representasi grafis dari himpunan yang menggunakan lingkaran atau bentuk tertutup lainnya untuk menggambarkan himpunan. Setiap lingkaran mewakili sebuah himpunan, dan area di mana lingkaran-lingkaran tersebut tumpang tindih menunjukkan elemen-elemen yang dimiliki bersama oleh himpunan-himpunan tersebut.
Contoh Penggunaan Diagram Venn
Contoh penggunaan diagram Venn dapat ditemukan dalam berbagai soal himpunan. Misalnya, jika kita memiliki dua himpunan A dan B, diagram Venn dapat digunakan untuk menggambarkan elemen-elemen yang unik pada A dan B, serta elemen-elemen yang sama pada kedua himpunan tersebut.
Dengan demikian, diagram Venn membantu dalam memahami konsep-konsep himpunan dengan lebih intuitif dan memudahkan dalam menyelesaikan masalah yang terkait dengan himpunan.
Prinsip Dasar Teori Himpunan
Aksioma Zermelo-Fraenkel menjadi landasan utama dalam pengembangan teori himpunan. Prinsip-prinsip ini memberikan dasar logis yang kuat untuk memahami berbagai konsep himpunan.
Aksioma Zermelo-Fraenkel
Aksioma Zermelo-Fraenkel adalah sekumpulan aksioma yang dirumuskan untuk membangun teori himpunan yang konsisten dan bebas dari paradoks. Aksioma ini mencakup prinsip-prinsip seperti aksioma ekstensionalitas, aksioma pasangan, dan aksioma tak terhingga.
Aksioma Ekstensionalitas menyatakan bahwa dua himpunan adalah sama jika dan hanya jika mereka memiliki elemen yang sama. Ini memberikan dasar untuk memahami kesetaraan himpunan.
Aksioma Tak Terhingga memungkinkan adanya himpunan tak terhingga, yang merupakan konsep penting dalam teori himpunan dan matematika modern.
Teorema Dasar dalam Teori Himpunan
Teorema-teorema dasar dalam teori himpunan, seperti Teorema Cantor-Bernstein-Schroeder, memainkan peran penting dalam memahami sifat-sifat himpunan. Teorema ini menyatakan bahwa jika terdapat dua himpunan A dan B, dan terdapat injeksi dari A ke B serta injeksi dari B ke A, maka A dan B memiliki kardinalitas yang sama.
Teorema ini memberikan alat penting untuk membandingkan ukuran himpunan dan memahami konsep kardinalitas.
Hubungan Teori Himpunan dengan Logika
Konsep logika memainkan peran penting dalam memahami teori himpunan. Logika himpunan membantu dalam menganalisis sifat-sifat himpunan dan relasi antara himpunan.
Dalam teori himpunan, logika digunakan untuk memahami berbagai konsep seperti union, intersection, dan complement himpunan. Dengan menggunakan logika, kita dapat memahami bagaimana operasi-operasi ini bekerja dan bagaimana mereka berinteraksi.
Konsep Logika dalam Teori Himpunan
Konsep logika dalam teori himpunan melibatkan penggunaan prinsip-prinsip logika untuk memahami sifat-sifat himpunan. Prinsip-prinsip ini termasuk hukum identitas, hukum komutatif, dan hukum distributif.
Dengan menggunakan konsep logika, kita dapat membuktikan berbagai teorema tentang himpunan dan memahami bagaimana mereka berhubungan dengan konsep matematika lainnya.
Penerapan Logika dalam Himpunan
Penerapan logika dalam himpunan membantu dalam memahami berbagai konsep matematika yang lebih kompleks. Logika himpunan digunakan dalam berbagai bidang seperti statistika, aljabar, dan informatika.
Dalam statistika, logika himpunan digunakan untuk memahami konsep-konsep seperti probabilitas dan distribusi. Dalam aljabar, logika himpunan membantu dalam memahami struktur aljabar dan operasi-operasi yang terkait.
Dengan demikian, logika himpunan memainkan peran penting dalam memahami berbagai konsep matematika dan aplikasinya dalam berbagai bidang.
Himpunan Fungsional
Himpunan fungsional memainkan peran penting dalam matematika karena berkaitan erat dengan konsep fungsi. Fungsi dapat dipandang sebagai relasi khusus antara himpunan, sehingga memahami himpunan fungsional menjadi kunci untuk memahami berbagai aplikasi matematika.
Fungsi dan Himpunan
Fungsi adalah pemetaan antara elemen-elemen dari satu himpunan ke himpunan lainnya. Dalam konteks ini, himpunan fungsional berkaitan dengan bagaimana fungsi tersebut didefinisikan dan bagaimana mereka beroperasi pada himpunan. Misalnya, fungsi f(x) = x^2 memetakan elemen-elemen dari himpunan bilangan real ke himpunan bilangan real non-negatif.
Berikut adalah beberapa aspek penting terkait fungsi dan himpunan:
- Fungsi dapat berupa injektif (satu-satu), surjektif (onto), atau bijektif (keduanya).
- Himpunan domain dan kodomain memainkan peran penting dalam definisi fungsi.
- Fungsi dapat digunakan untuk memodelkan berbagai fenomena dalam matematika dan ilmu lainnya.
Contoh Himpunan Fungsional
Contoh himpunan fungsional dapat ditemukan dalam berbagai cabang matematika. Misalnya, dalam aljabar, himpunan semua matriks 2×2 dengan operasi penjumlahan matriks membentuk sebuah grup abelian, yang merupakan contoh himpunan fungsional.
Berikut adalah beberapa contoh lainnya:
- Himpunan semua fungsi kontinu pada interval [a, b] dengan operasi penjumlahan fungsi.
- Himpunan semua polinomial dengan koefisien real.
- Himpunan semua transformasi linier dari ruang vektor V ke ruang vektor W.
Dalam setiap contoh di atas, himpunan fungsional memainkan peran sentral dalam memahami struktur dan sifat-sifat matematika yang terkait.
Teori Himpunan dalam Statistika
Penerapan teori himpunan dalam statistika telah membuka jalan bagi metode analisis yang lebih canggih. Dalam statistika, konsep-konsep seperti ruang sampel dan kejadian sangat bergantung pada teori himpunan.
Penerapan Teori Himpunan dalam Statistika
Teori himpunan digunakan untuk memahami dan menganalisis data dalam statistika. Dengan menggunakan prinsip-prinsip himpunan, statistika dapat mengidentifikasi pola dan hubungan dalam data yang kompleks.
Konsep dasar seperti union, intersection, dan complement digunakan untuk mengolah data dan membuat keputusan yang tepat.
Contoh Kasus di Statistika
Contoh penerapan teori himpunan dalam statistika dapat dilihat dalam analisis risiko dan peluang. Dengan menggunakan diagram Venn, statistika dapat memvisualisasikan hubungan antara berbagai kejadian dan membuat prediksi yang lebih akurat.
Dalam statistika, teori himpunan tidak hanya membantu dalam analisis data, tetapi juga dalam pengambilan keputusan yang berbasis data.
Teori Himpunan dan Aljabar
Teori himpunan dan struktur aljabar memiliki hubungan yang sangat signifikan dalam pengembangan matematika modern. Himpunan dapat digunakan untuk memahami konsep-konsep aljabar seperti grup dan ring, yang merupakan dasar dari berbagai struktur aljabar.
Hubungan Himpunan dan Struktur Aljabar
Dalam aljabar, himpunan digunakan untuk mendefinisikan operasi-operasi dasar seperti penjumlahan dan perkalian. Struktur aljabar seperti grup dan ring dibangun di atas himpunan dan operasi-operasi ini.
Contohnya, sebuah grup didefinisikan sebagai himpunan yang dilengkapi dengan operasi biner yang memenuhi sifat-sifat tertentu seperti asosiatif, memiliki elemen identitas, dan setiap elemen memiliki invers.
Aplikasi dalam Penyelesaian Masalah
Aplikasi teori himpunan dalam aljabar membantu dalam memahami sifat-sifat aljabar dan penyelesaian masalah. Dengan menggunakan konsep himpunan, kita dapat menganalisis struktur aljabar dan memahami bagaimana mereka berinteraksi.
| Struktur Aljabar | Definisi | Contoh |
|---|---|---|
| Grup | Himpunan dengan operasi biner yang memenuhi sifat asosiatif, memiliki elemen identitas, dan setiap elemen memiliki invers. | Grup bilangan bulat dengan operasi penjumlahan. |
| Ring | Himpunan dengan dua operasi biner (penjumlahan dan perkalian) yang memenuhi sifat-sifat tertentu. | Ring bilangan bulat dengan operasi penjumlahan dan perkalian. |
Dengan memahami hubungan antara teori himpunan dan aljabar, kita dapat lebih efektif dalam menganalisis dan menyelesaikan masalah-masalah yang kompleks dalam matematika.
Penerapan Teori Himpunan dalam Informatika
Teori himpunan menjadi dasar bagi beberapa struktur data dalam informatika. Dengan memahami konsep himpunan, para pengembang dapat menciptakan algoritma yang lebih efisien dan struktur data yang lebih efektif.
Himpunan dalam Struktur Data
Dalam informatika, himpunan digunakan dalam berbagai struktur data seperti set dan map. Struktur data ini memungkinkan penyimpanan dan pengolahan data dengan lebih efisien.

Penggunaan himpunan dalam struktur data membantu dalam pengurangan kompleksitas waktu dan meningkatkan kinerja sistem.
Algoritma yang Menggunakan Himpunan
Banyak algoritma yang memanfaatkan konsep himpunan untuk menyelesaikan masalah komputasi dengan lebih efisien. Contohnya, algoritma untuk mencari union dan intersection himpunan digunakan dalam berbagai aplikasi.
- Algoritma untuk penggabungan himpunan (union) digunakan dalam penggabungan data.
- Algoritma untuk irisan himpunan (intersection) digunakan dalam pencarian data yang sama.
Dengan demikian, teori himpunan memainkan peran penting dalam pengembangan algoritma yang efektif.
Tantangan dan Problematika dalam Teori Himpunan
Teori himpunan, meskipun sangat fundamental dalam matematika, juga memiliki beberapa tantangan yang perlu dipecahkan. Dalam perkembangan teori himpunan, beberapa masalah telah muncul dan menjadi fokus perhatian para matematikawan.
Masalah-masalah ini seringkali berkaitan dengan dasar-dasar teori himpunan itu sendiri, seperti definisi himpunan dan operasi-operasi yang berlaku di dalamnya.
Masalah Umum dalam Teori Himpunan
Salah satu masalah paling terkenal dalam teori himpunan adalah paradoks Russell, yang ditemukan oleh Bertrand Russell pada awal abad ke-20. Paradoks ini menunjukkan adanya kontradiksi dalam definisi himpunan yang terlalu luas.
Paradoks ini memicu perdebatan tentang bagaimana seharusnya himpunan didefinisikan dan bagaimana menghindari kontradiksi-kontradiksi semacam itu.
Solusi dan Strategi
Untuk mengatasi masalah-masalah tersebut, beberapa solusi dan strategi telah dikembangkan. Salah satu pendekatan yang umum digunakan adalah Aksioma Zermelo-Fraenkel, yang memberikan dasar yang lebih kokoh untuk teori himpunan.
Aksioma ini membantu dalam menghindari paradoks-paradoks dengan membatasi definisi himpunan dan operasi-operasi yang diperbolehkan.
Selain itu, pengembangan teori himpunan yang lebih modern juga melibatkan konsep-konsep seperti himpunan bagian dan operasi himpunan yang lebih kompleks.
Dengan demikian, teori himpunan terus berkembang dan menjadi lebih kuat dalam menghadapi tantangan-tantangan yang ada.
Kesimpulan
Teori himpunan telah dibahas secara komprehensif dalam artikel ini, mencakup pengertian dasar hingga aplikasinya dalam berbagai disiplin ilmu. Dengan memahami rangkuman teori himpunan, pembaca dapat melihat bagaimana konsep ini menjadi fondasi penting dalam matematika dan bidang lainnya.
Poin Utama Teori Himpunan
Rangkuman teori himpunan mencakup berbagai aspek, mulai dari definisi hingga operasi himpunan. Pemahaman yang baik tentang teori ini memungkinkan pengembangan lebih lanjut dalam berbagai aplikasi.
Implikasi dan Pengembangan
Implikasi teori himpunan terlihat dalam berbagai bidang seperti statistika, aljabar, dan informatika. Dengan terus berkembangnya matematika dan aplikasinya, teori himpunan akan tetap menjadi konsep yang relevan dan penting.
Dengan demikian, pemahaman yang mendalam tentang teori himpunan tidak hanya memperkaya pengetahuan matematika tetapi juga membuka peluang bagi inovasi di masa depan.
FAQ
Apa itu teori himpunan?
Teori himpunan adalah cabang matematika yang mempelajari tentang kumpulan objek yang unik dan memiliki sifat tertentu.
Apa pengertian himpunan dalam matematika?
Himpunan dalam matematika didefinisikan sebagai kumpulan objek yang unik dan memiliki sifat tertentu, digunakan sebagai dasar untuk memahami berbagai konsep matematika.
Bagaimana notasi himpunan digunakan dalam matematika?
Notasi himpunan digunakan untuk menyatakan relasi antara elemen dan himpunan, serta untuk mengoperasikan himpunan dengan menggunakan simbol-simbol seperti ∈, ⊆, dan ∪.
Apa perbedaan antara himpunan berhingga dan himpunan tak terhingga?
Himpunan berhingga memiliki jumlah elemen yang terbatas, sedangkan himpunan tak terhingga memiliki jumlah elemen yang tidak terbatas.
Bagaimana teori himpunan digunakan dalam statistika?
Teori himpunan digunakan dalam statistika untuk memahami konsep-konsep seperti ruang sampel dan kejadian, serta untuk analisis data dan pengambilan keputusan.
Apa itu diagram Venn dan bagaimana penggunaannya?
Diagram Venn adalah alat visual yang digunakan untuk menggambarkan relasi antara himpunan, membantu memahami konsep-konsep seperti union, intersection, dan complement.
Bagaimana teori himpunan terkait dengan logika?
Teori himpunan memiliki hubungan erat dengan logika, karena konsep logika digunakan dalam memahami dan mengoperasikan himpunan.
Apa itu himpunan fungsional?
Himpunan fungsional berkaitan dengan konsep fungsi dalam matematika, yaitu relasi khusus antara himpunan.
Bagaimana teori himpunan digunakan dalam informatika?
Teori himpunan digunakan dalam informatika, terutama dalam struktur data dan algoritma, seperti set dan map.
Apa saja tantangan dan problematika dalam teori himpunan?
Tantangan dan problematika dalam teori himpunan meliputi masalah umum seperti paradoks Russell dan masalah aksioma himpunan.
