Pemahaman Dasar Trigonometri: Contoh Soal dan Pembahasan

Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam segitiga. Konsep ini sangat penting dalam berbagai bidang, seperti fisika, teknik, astronomi, dan geometri. Dalam artikel ini, kita akan membahas dasar trigonometri, termasuk identitas dasar, fungsi trigonometri, serta contoh soal dan pembahasannya.

Konsep Dasar Trigonometri

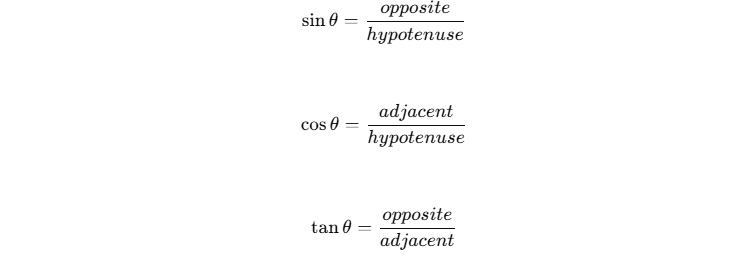
Trigonometri berkaitan erat dengan segitiga siku-siku. Tiga fungsi utama dalam trigonometri adalah:

1. Sinus (sin): perbandingan antara panjang sisi depan sudut terhadap panjang sisi miring.
2. Kosinus (cos): perbandingan antara panjang sisi samping sudut terhadap panjang sisi miring.
3. Tangen (tan): perbandingan antara panjang sisi depan sudut terhadap panjang sisi samping.

Hubungan ini dapat dirumuskan sebagai berikut:

Identitas Trigonometri Dasar

Beberapa identitas trigonometri yang penting untuk diingat:

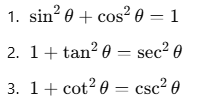
Identitas ini sangat berguna dalam menyederhanakan dan menyelesaikan berbagai soal trigonometri.

Contoh Soal dan Pembahasan

Contoh Soal 1

Diketahui sebuah segitiga siku-siku dengan panjang sisi miring 10 cm dan panjang salah satu sisi yang berhadapan dengan sudut adalah 6 cm. Tentukan nilai , , dan !

Pembahasan: Diketahui:

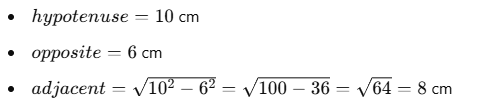
Maka:

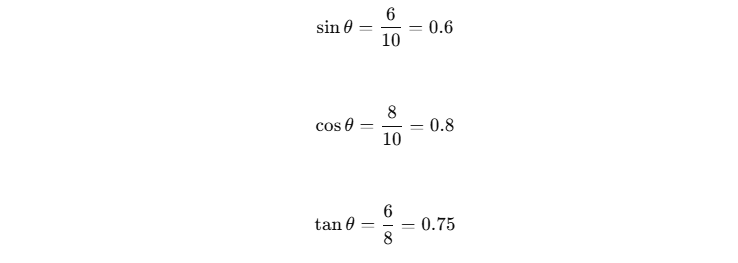
Contoh Soal 2

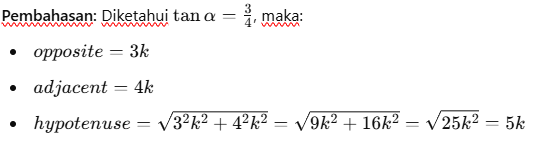
Maka:

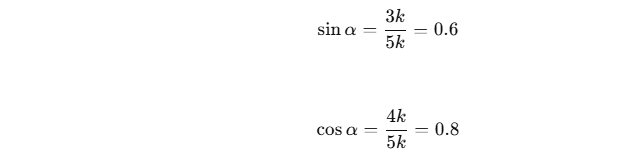
Penerapan Dasar Trigonometri dalam Kehidupan Sehari-hari

Trigonometri sering digunakan dalam berbagai bidang, antara lain:

1. Arsitektur: Menghitung tinggi bangunan atau sudut kemiringan atap.
2. Astronomi: Menentukan jarak antara bintang dan planet.
3. Teknik Sipil: Menghitung panjang jembatan atau ketinggian menara.
4. Navigasi: Digunakan dalam sistem GPS untuk menentukan posisi suatu tempat.
5. Oseanografi: Digunakan untuk menghitung tinggi gelombang laut.

Peran Dasar Trigonometri dalam Teknologi Modern

Selain penerapan dasar trigonometri dalam ilmu teknik dan sains, konsep ini juga digunakan dalam pengembangan teknologi modern seperti:

• Pemrograman Grafis: Trigonometri digunakan untuk membuat animasi dan model 3D.
• Robotika: Membantu perhitungan gerakan dan posisi robot di ruang 3D.
• Pemrosesan Sinyal: Digunakan dalam sistem komunikasi untuk pemrosesan data dan suara.

Tips Menguasai Dasar Trigonometri

Untuk menguasai dasar trigonometri, beberapa tips yang bisa diterapkan adalah:

1. Pahami konsep dasar: Menghafal rumus saja tidak cukup, pemahaman konsep sangat penting.
2. Latihan soal: Mengerjakan berbagai jenis soal akan memperkuat pemahaman.
3. Gunakan alat bantu: Kalkulator dan software matematika bisa membantu eksplorasi konsep.
4. Terapkan dalam kehidupan nyata: Mencoba menerapkan konsep trigonometri dalam masalah sehari-hari akan memperdalam pemahaman.

Kesimpulan

Pemahaman dasar tentang trigonometri sangat penting dalam menyelesaikan berbagai persoalan matematika dan kehidupan nyata. Dengan memahami konsep fungsi trigonometri dan identitasnya, kita dapat dengan mudah menyelesaikan berbagai persoalan yang melibatkan segitiga dan sudut. Dasar trigonometri tidak hanya berguna dalam akademik tetapi juga dalam teknologi modern yang semakin berkembang.